Describe How to Add Two Vectors Using Their Components

This video goes through breaking them down and adding the components. Adding Vectors Using Component Method Consider adding three 2-D vectors A B and C.

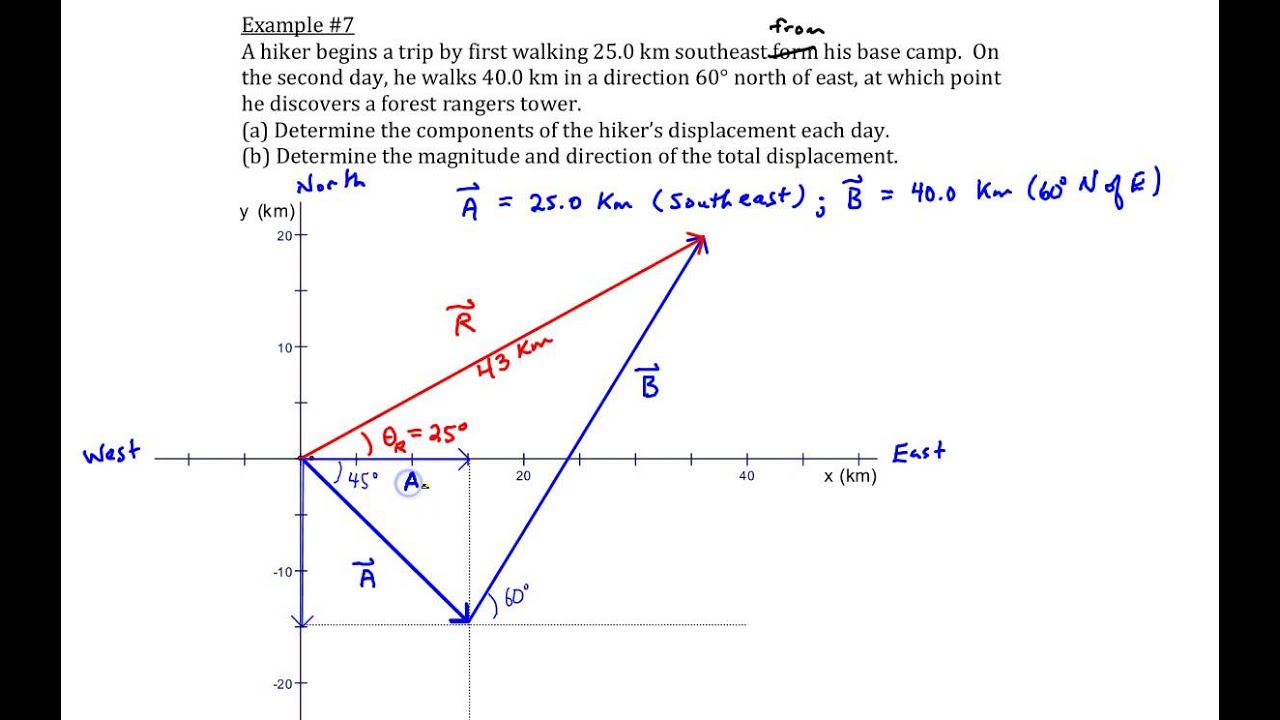
Chapter 1 Example 7 Component Method Of Vector Addition Youtube

Two vectors a and b represented by the line segments can be added by joining the tail of vector b to the nose of vector a.

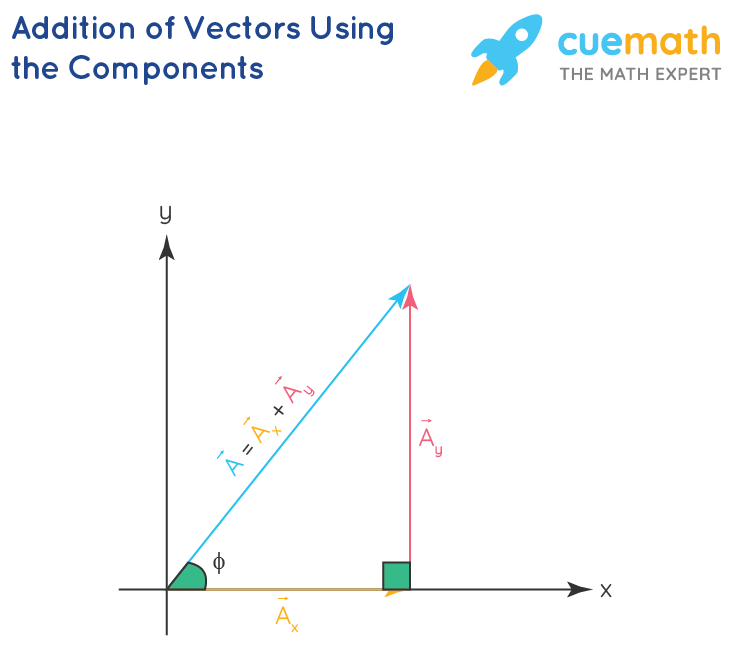
. Place the next vector with its tail at the previous vectors head. The tail of the vector is the starting point of the vector and the head or tip of a vector is the pointed end of the arrow. An example of how to add two vectors by using their components.

A A xi A yj B B xi B yj C C xi C yj 1. Add the x-components and y-components of each vector to obtain the resultant vector R in unit vector notation. Slide the vectors keeping the orientation the same until they connect nose-to-tail and then take the resultant as being from the free tail to the free head.

That means that the vector addition formula in 2D is as follows. This video goes through breaking them down and adding the components. To multiply a vector by a scalar.

S m1n1 m2 n2. How to add vectors using components part 1 An example of how to add two vectors by using their components. U v u v u 1 v 1 u 2 v 2.

As a matter of fact adding vectors is really easy especially when we have Cartesian coordinates. To be precise we simply add the numbers coordinate-wise. Vector addition is one of the most common vector operations that a student of physics must master.

M m1 m2 N n1 n2 Performing vector addition on the two vectors is equivalent to adding the two vectors respective x and y components. Let the x-axis represent the east-west direction. Abc def a d b e c f.

Learn how to add vectors. The graphical method of adding vectors A and B involves drawing vectors on a graph and adding them using the head-to-tail method. 3 Likewise multiplying a vector by a number is straightforwardly expressed in terms of components r r x x r y y r z z.

For example consider the two vectors M and N given as. Consider two vectors making angles q 1 and q 2 with ve x-axis respectively. Vectors can be added using the nose-to-tail method or head-to-tail method.

The resultant vector R is defined such that A B R. The first thing we must realise is that the order that we add the vectors does. The head-to-tail method is a graphical way to add vectors.

The set-up was done in part 1. Adding Vectors Using Components Step 1. To find the magnitude and direction of a vector when given its components.

Resolve F 1 F 1 into components. The magnitude and direction of R are then determined with a ruler and protractor respectively. Let u u 1 u 2 and v v 1 v 2 be two vectors.

Then the vector sum of rand wis given simply by adding components r w r x w x x r y w y y r z w z z. To define the terms vector magnitude component. Alternatively the tail of vector a can be joined to the nose of vector b.

And so forth until all vectors have been added. Calculate the magnitude of the. Rectangular component method of addition of vectors is the most simplest method to add a number of vectors acting in different directions.

Adding vectors using their components For more than two vectors we can use the components of a set of vectors to find the components. When adding vectors a head-to-tail method is employed. To add or subtract two vectors add or subtract the corresponding components.

To add vectors lay the first one on a set of axes with its tail at the origin. Sx m1 n1. The following steps describe how to use the head-to-tail method for graphical vector addition.

To add two vectors using the head-to-tail method. Drag vectors onto a graph change their length and angle and sum them together. Will explain and give examples of what is a vector and how is used in math and physics.

To add two or more vectors using components. U v u 1 v 1 u 2 v 2. To add two vectors using the parallelogram method.

The magnitude angle and components of each vector can be displayed in several formats. How to add vectors using components part 2 Finish up a problem dealing with adding vectors using components. This yields the resultant vector S.

Vector x component x-hat y component y-hat where x-hat and y-hat represent vectors with a length of 1 pointing alongparallel to the positive x-axis and positive y-axis respectively. Decide how to tackle the problem. Resolve vector into two rectangular components and.

Ab de a d b e and the one in 3D is. R A B C A xi A yj B xi B yj C xi C yj R A x B x C x i A y B y C y j R R 2. Up to 10 cash back Adding and Subtracting Vectors.

Resolve vector into two rectangular components and. The difference of u and v is. 4 Additionally two vectors are equal to each other if and only if all three of their.

To break a vector into components. The same way you add two non-parallel vectors. The addition of the vectors is the diagonal through the first vertexOtherwise and more accuratelyif you have vectors a and b inclined at angles p and q to the positive direction of the x axis then the component of their sum along thehorizontal direction is s acosp bcosqand the vertical component is t asinp bsinqThe magnitude of the resultant is.

When there are no more vectors draw a straight line from the origin to the head of the last vector. Then the sum of u and v is the vector. S M N.

Hope this helps and does not mislead or confuse you. It can be written explicitly as. We find the components of F 1.

This line is the sum of the vectors. The head of the second vector is placed at the tail of the first vector and the head of the third vector is placed at the tail of the second vector.

Addition Of Vectors By Means Of Components Physics Youtube

The Component Method Of Finding A Resultant Youtube

Vector Addition Formula Laws Sum Addition Of Vectors